
What is the CAP theorem? It is actually a misnomer and a poorly understood result of distributed systems theory. Let’s start with the story. In 2000, Eric Brewer from UC Berkeley gave a keynote talk at the ACM Conference on Principles of Distributed Computing (PODC) where he presented the conjecture that out of three properties, namely Consistency, Availability and Partition tolerance (CAP), only two could be achieved in a distributed system subject to partitions [Brewer 2000]. Later, Seth Gilbert and Nancy Lynch from MIT, instantiated the conjecture, which was very broad and general, for a particular case – a replicated read-write register, and came up with a theorem and proof [Gilbert & Lynch 2002]. More recently, Eric Brewer wrote an article discussing the misunderstandings on the CAP theorem and explaining in depth the technical implications of CAP [Brewer 2012].
The CAP theorem talks about the tradeoffs if one wishes to provide partition tolerance in a distributed system with data replication (or a replicated system). It has been used by many NoSQL database vendors (mainly key-value data stores and document data stores, see our blog post on SQL, NoSQL & NewSQL) as a justification for not providing transactional ACID consistency (see our blog post on Understanding the ACID properties of transactions and underlying principles), claiming that the CAP theorem “proves” that it is impossible to provide scalability and ACID consistency at the same time. However, a closer look at the CAP theorem and, in particular, the formalization by Gilbert & Lynch, reveals that the CAP theorem does not refer at all to scalability (there is no S in CAP!), but only availability (the A in CAP).
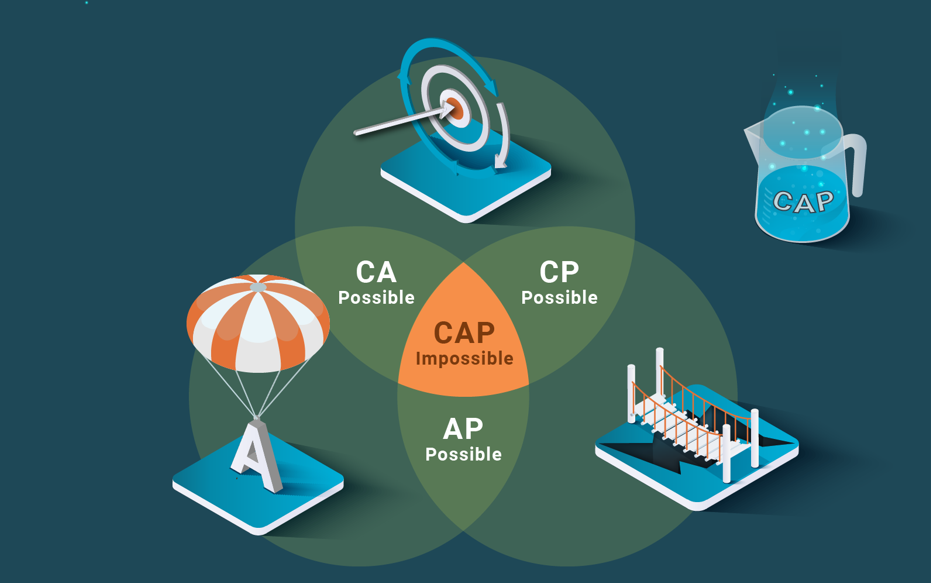
What the CAP theorem actually states is that a replicated system that tolerates partitions can only deliver CA or CP. Thus, the claim that it is impossible to provide scalability and ACID consistency is just false. It is quite interesting that most practitioners accepted the claim as ground truth without actually reading the original paper.
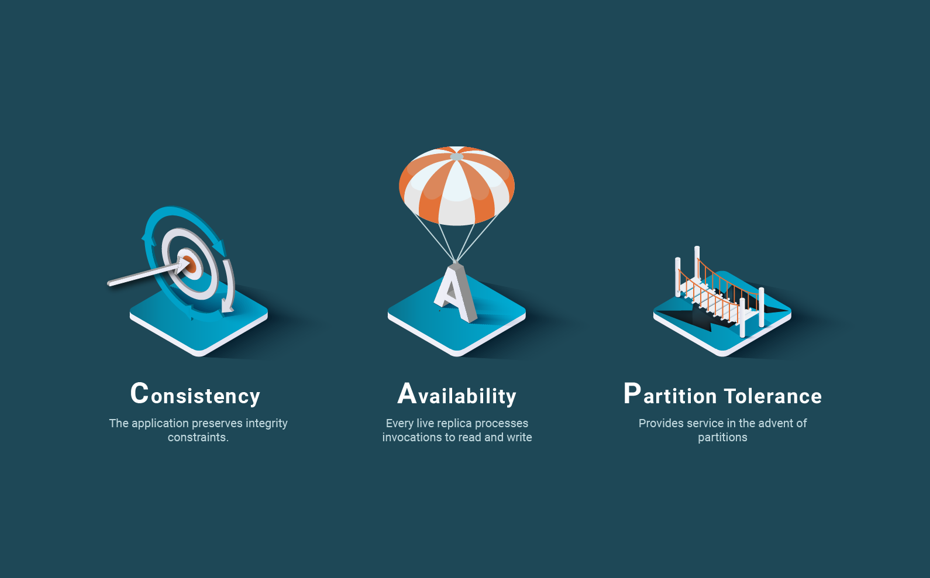
Let’s analyze each of the three properties in CAP. Consistency (C) is an overloaded term that means too many different things. The term is used to define the coherence of data in the presence of different problems: concurrent accesses (which requires what is termed isolation in databases or linearizability in distributed systems or safety in concurrent programming), failures during updates of persisted data (which requires atomicity, i.e. that all updates of a transaction are applied to persisted data or none in the presence of failures), node failures in a replicated system (which requires replica consistency such as 1-copy serializability), breaking integrity constraints, etc. Without a rigorous and precise definition, talking about consistency is useless. In the CAP theorem, which deals with data replication (the only way to attain A, Availability), consistency actually refers to data consistency across replicas. However, there are different consistency criteria for replicated data.
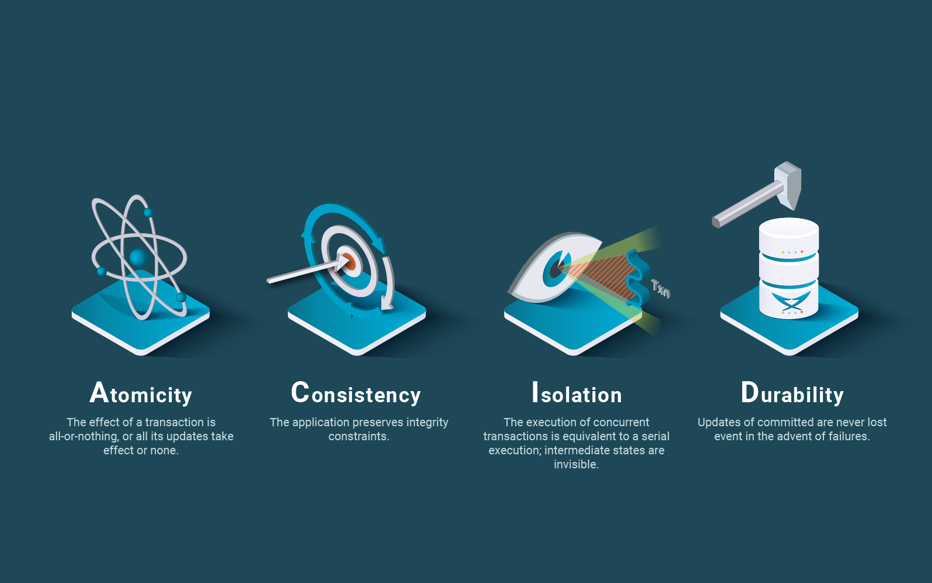
In his presentation [Brewer 2000], for which only slides are available, Brewer does not define consistency, but only discusses two main approaches to consistency: ACID (Atomicity, Consistency, Isolation, Durability) in the database community and BASE (Basically Available, Soft state, Eventual consistency) in the distributed system community. It should be noted that he is comparing apples with pears, since BASE considers replication and ACID by itself alone, does not.
Let’s look at different notions of consistency for data replication. In ACID databases, 1-copy consistency [Özsu & Valduriez 2020] states that a replicated database should behave as a non-replicated database, i.e. replication is transparent and does not introduce unexpected results such as inconsistencies. 1-copy consistency has been applied to serializability, a consistency criterion for concurrent execution of transactions over data. 1-copy serializability is the actual consistency criterion for replicated databases based on locking. While 1-copy snapshot isolation [Yin et al., 2009] is the criterion for replicated databases based on multi-version concurrency control (MVCC) isolation criterion, called snapshot isolation.
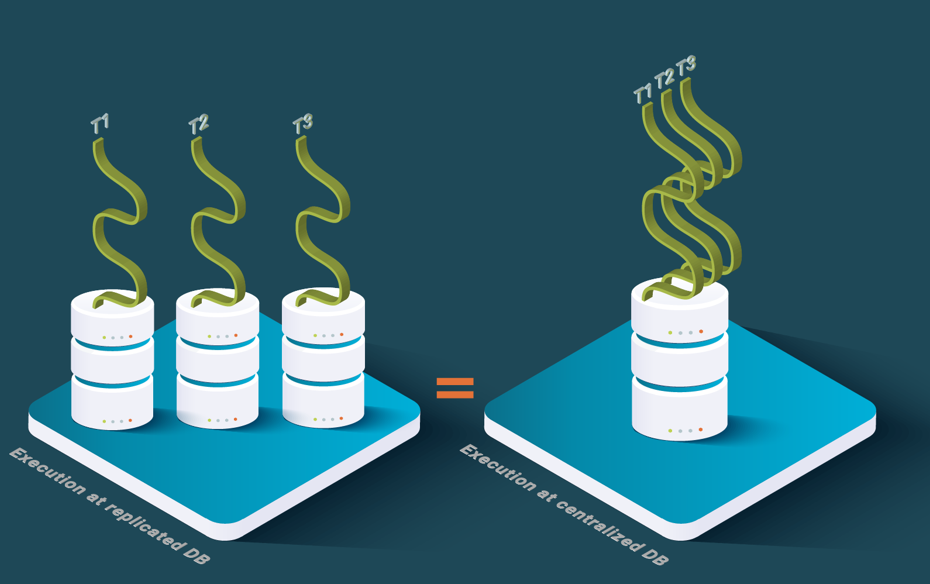
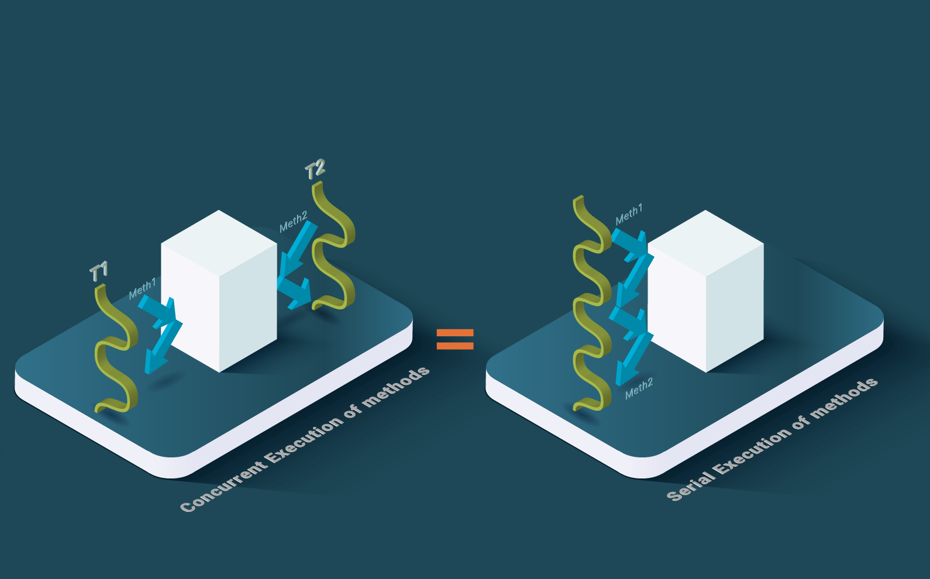
In distributed systems, the notions of consistency for concurrent execution are much more relaxed. One commonly used notion is linearizability, which states that the concurrent execution of methods over an object should be equivalent to a linear (sequential) sequence of invocations of these methods over the object. Linearizability is often used for replicated objects and we could use the term 1-copy linearizability if necessary.
So, what does the CAP theorem tell us? In fact, something that is well known in distributed systems. If you want to tolerate partitions in a replicated system, there are only two approaches: primary-component and partitionable. With the primary-component approach, only the partition with a majority of replicas is allowed to progress. For instance, with 3 replicas and 2 partitions, only the partition with 2 replicas (called the majority partition) will continue to work. Minority partitions, e.g. the partition with 1 replica, are blocked until the partition is healed. The partitionable approach allows partitions to work independently so they diverge. When the partition is healed, their replicas must be reconciled. In the example above, the partitions with one and 2 replicas will progress independently, leading to different replica values. When the partition is healed, it is necessary to decide what value to take. However, reconciliation is hard, as it depends on the business logic and is not always possible. The main issue is that during reconciliation, there can be node failures and more partitions, which require doing reconciliation in any combination of failures and partitions.
In the primary-component approach (called CP in CAP), replica consistency can be achieved as follows. Basically, the replicated system continues working in the primary component that contains a majority of the original replicas. However, the minority partitions are blocked. Thus, the replicas in the minority partitions (like the partition with a single replica before) do not satisfy the availability requirement that if a client connects to them, they have to reply immediately, but they cannot because they are blocked by design.

In the partitionable approach (called CA in CAP), consistency is lost because each partition evolves independently and that cannot satisfy the 1-copy consistency semantics since the replicated system is not delivering the answers, it should behave as would a non-replicated system.

Now, let us go deeper into the theorem proven in [Gilbert & Lynch 2002]. The theorem uses a register as data abstraction. A register is an object that has two methods: set and get. It formalizes the notion of consistency of the CAP theorem as linearizability or, to be precise, 1-copy linearizability, the extension of linearizability to a replicated object. Availability is formalized as the ability to connect to any replica of the object, which should reply immediately to the method invocation (i.e. without waiting for a partition to heal). Partitioning is formalized as a fully asynchronous system, i.e. a system that can partition. The theorem demonstration is based on a very important result in distributed systems theory, the impossibility result of solving consensus in asynchronous systems in which at least one node can fail. In the core of this result, it is the impossibility of distinguishing a failed node from a partitioned node. Due to the impossibility of making this distinction, consensus cannot be completed since it has the requirement to reach agreement among all non-failed nodes.
This situation prevents an agreement from being reached among all non-failed nodes for every write. Without being able to reach agreement (consensus), any system will have to choose between consistency and availability. To attain consistency, what is done it is to take a primary-component approach where only a majority partition of replicas can progress without waiting for the minority partitions that will get blocked. The minority partitions will not be fulfilling availability, which requires them to reply to any client request, because they block to avoid two states of the replicated data to evolve independently. Note that there can be only one primary partition, since it is not possible to have two disjoint majorities over the same set of replicas, they will have to overlap on at least one node. In summary, the primary-component approach results in choosing CP, at the loss of A.
If one chooses not to wait for consensus to complete, all partitions will be updated independently and the reads will return the local values that cannot be consistent because it is impossible that the replicas behave as a non-replicated system, since each partition will only observe the local writes but not the writes on the other partitions. This means that one is choosing AP, at the loss of C.
Main takeaways
The CAP theorem is about the alternative approaches one can choose to deal with partitions in a replicated system: primary-component or partitionable. In a primary-component system, only the majority partition is allowed to progress, by processing requests, and minority partitions are blocked. This results in providing CP but losing A. In a partitionable system, all partitions continue processing requests but since they cannot communicate, they lose C, but deliver AP. Thus, the CAP theorem has nothing to do with the scalability of ACID systems, and nothing to do with any scalability. There is no S in CAP.
References
[Brewer 2000] Eric Brewer. Towards robust distributed systems (keynote talk). Int. Conference on Principles of Distributed Systems (PODC), 2000.
[Brewer 2012] Eric Brewer. CAP Twelve years later: How the “Rules” have Changed. Computer 45(2):23-29. Feb. 2012.
[Fischer et al., 1985] Michael J. Fischer, Nancy A. Lynch, and Michael S. Paterson. 1985. Impossibility of distributed consensus with one faulty process. Journal of the ACM, 32(2) 374–382, 1985.
[Gilbert & Lynch 2002] Seth L. Gilbert, Nancy A. Lynch. Brewer’s conjecture and the feasibility of consistent, available, partition-tolerant web services. ACM SIGACT News, 2002.
[Özsu & Valduriez 2020] Tamer Özsu, Patrick Valduriez. Principles of Distributed Database Systems, 4th Edition, Springer, 2020.
[Yin et al., 2009] Yi Lin, Bettina Kemme, Ricardo Jiménez-Peris, Marta Patiño-Martínez, José Armendariz. Snapshot isolation and integrity constraints in replicated databases. ACM Transactions on Database Systems (TODS), 34 (2), 1-49, 2009.
ABOUT THIS BLOG SERIES
This blog series aims at educating database practitioners in topics commonly not well understood, often due to false or confusing marketing messages. The blog provides the foundations and tools to let the reader actually evaluate databases, learn their real capabilities and be able to compare the performance of the different alternatives for its targeted workload. The blog is vendor agnostic.
ABOUT THE AUTHORS
- Dr. Ricardo Jimenez-Peris is the CEO and founder of LeanXcale. Before founding LeanXcale, he was for over 25 years a researcher in distributed databases director of the Distributed Systems Lab and university professor teaching distributed systems.
- Dr. Patrick Valduriez is a researcher at INRIA, co-author of the book “Principles of Distributed Databases” that has educated legions of students and engineers in this field and more recently, Scientific Advisor of LeanXcale.
ABOUT LEANXCALE
LeanXcale is a startup making a NewSQL database. Since the blog is vendor agnostic, we do not talk about LeanXcale itself. Readers interested on LeanXcale can visit LeanXcale website.
